На корме массой m стоит матрос массой m

№ 12105
Три лодки массами 100 кг каждая идут одна за другой с одинаковыми скоростями. Из средней лодки одновременно в переднюю и заднюю бросают горизонтально со скоростью 2,2 м/с относительно лодки грузы массой 10 кг каждый. Найдите величину относительной скорости (в см/с) передней и задней лодок после попадания в них грузов.
№ 12106
От поезда, идущего с постоянной скоростью 64 км/ч, отделяется пятая часть состава. Через некоторое время скорость отделившихся вагонов уменьшилась в 2 раза. Считая, что сила тяги при разрыве не изменилась, найдите скорость (км/ч) головной части поезда в этот момент. Сила трения пропорциональна весу.
№ 12107
Снаряд, летящий с некоторой скоростью, распадается на два осколка. Скорость большего осколка по величине равна начальной скорости снаряда и направлена перпендикулярно к ней. Скорость другого осколка по величине в 5 раз больше первоначальной. Найдите отношение масс осколков.
№ 12108
Снаряд массой 50 кг, летящий под углом 30° к вертикали со скоростью 600 м/с, попадает в платформу с песком и застревает в ней. Найдите скорость платформы после попадания снаряда. Масса платформы 950 кг. Трением между платформой и рельсами пренебречь.
№ 12109
В ящик с песком массой 9 кг, соскальзывающий с гладкой наклонной плоскости, попадает горизонтально летящее ядро массой 3 кг и застревает в нем. Найдите скорость ящика сразу же после попадания ядра, если непосредственно перед попаданием скорость ящика равнялась 6 м/с, а скорость ядра 12 м/с. Угол наклона плоскости к горизонту 60°.
№ 12110
Небольшое тело массой 190 г лежит на вершине гладкой полусферы радиусом 90 см. В тело попадает пуля массой 10 г, летящая горизонтально, и застревает в нём. При какой минимальной скорости пули тело после этого сразу оторвётся от поверхности полусферы?
№ 12111
Тележка стоит на гладких рельсах. Человек переходит с одного её конца на другой параллельно рельсам. На какое расстояние относительно земли переместится при этом тележка? Масса человека 60 кг, масса тележки 120 кг, её длина 6 м.
№ 12610
Доска массой M движется равномерно по гладкой горизонтальной поверхности со скоростью υ. Сверху на доску осторожно кладут кирпич массой m = M/2. Какое расстояние пройдет кирпич по доске за время проскальзывания? Коэффициент трения между доской и кирпичом равен μ.
№ 12611
Плот массой M свободно скользит по поверхности воды со скоростью υ. С берега на плот прыгает человек массой m, скорость которого в горизонтальном направлении равна u. Пренебрегая погружением плота при толчке, определите его скорость вместе с человеком для случаев, когда скорости человека и плота направлены в одну сторону, в противоположные, перпендикулярно друг другу. Трением плота о воду пренебречь.
№ 12612
На корме шлюпки массой M стоит матрос массой m. Длина шлюпки l. В некоторый момент времени матрос начинает идти на нос шлюпки со скоростью υ относительно лодки. Считая силу сопротивления воды постоянной и равной F, определите: а) скорость шлюпки в зависимости от времени; б) расстояние, на которое сместится матрос, перейдя с кормы на нос шлюпки.
№ 12613
Гладкий неупругий шарик из мягкого свинца налетает на такой же шарик, находящийся в покое. Скорость первого шарика в момент удара направлена под углом α к линии центров шаров. Под каким углом разлетятся шары после удара?
№ 12614
На горизонтальной плоскости сделан выстрел из винтовки. Ствол винтовки был поднят под углом 30° к горизонту, и пуля массой 10 г попала в вагончик массой 2 кг, шедший со скоростью 1 м/с навстречу пуле. Определите скорость вагончика после удара пули, если известно, что она попадает в него на расстоянии 100 м от места выстрела и что конец ствола и вагончик находятся на одном уровне. Как изменится ответ, если в момент удара пули вагончик будет удаляться от места выстрела?
№ 12615
Из орудия выстрелили вертикально вверх. Снаряд вылетел из ствола со скоростью υ0 и в верхней точке разорвался на два одинаковых осколка. Первый осколок упал со скоростью υ1 недалеко от места выстрела. Через сколько времени упадут первый и второй осколки?
№ 12616
Снаряд, выпущенный под углом к горизонту, разорвался в верхней точке траектории на два осколка, отношение масс которых равно n. Один осколок после разрыва полетел горизонтально и упал недалеко от места выстрела. Определите, на каком расстоянии x от этого осколка упадёт второй осколок, если точка разрыва удалена по горизонтали от места выстрела на расстояние S.
№ 12617
При неудачном запуске ракеты под некоторым углом к горизонту она разорвалась в верхней точке траектории на высоте 400 м на две одинаковые части. Через 2 с после разрыва одна часть падает на землю под тем местом, где произошел взрыв. На каком расстоянии от места старта упадет второй осколок, если первый упал на расстоянии 1 км от стартовой площадки?
№ 12618
Через легкий блок, вращающийся на оси без трения, перекинута нить, на концах которой привязаны грузы одинаковой массы M. Один из концов нити пропущен через кольцо массой m, укрепленное на высоте h от соответствующего груза. В некоторый момент времени кольцо падает и остается на грузе. Определите время, за которое расстояние между грузами станет равным 2h.
№ 12620
Две лодки массой M, на каждой из которых находилось по одному человеку массой m, двигались равномерно навстречу друг другу параллельными курсами. В тот момент, когда лодки поравнялись, из каждой из них в другую перешел человек. После этого лодки двигались в прежних направлениях со скоростями u1 и u2. Чему были равны начальные скорости лодок?
№ 12621
С неподвижного ракетного катера массой M выпущены одна за другой n ракет массой m каждая. Пренебрегая сопротивлением воды, определите, какую скорость будет иметь катер, если скорость ракет относительно катера в горизонтальном направлении равна u.
№ 12622
Лыжник массой M, скользящий с горы, у которой длина спуска равна l и наклон к горизонту α, на половине пути стреляет вертикально вверх. Ракета массой m « M вылетает из ракетницы со скоростью u. Определите скорость лыжника в конце спуска. Трением пренебречь.
№ 12624
Человек, находящийся в лодке, движущейся со скоростью υ = 1 м/с, прыгает с кормы в воду под углом α = 30° к горизонту со скоростью u = 5 м/с относительно лодки. Масса лодки M = 180 кг, масса человека m = 60 кг. Определите: а) дальность прыжка; б) угол, под которым должен прыгнуть человек, чтобы дальность прыжка была наибольшей.
Источник
Физика /1.Теоретическая физика
К.п.н. Мищик С.А.
Государственный морской университет имени адмирала Ф.Ф.Ушакова ,
Россия
Системные задачи динамической прикладной физики
морского флота
Системные задачи динамической прикладной физики морского флота отражают целостно-системное моделирование основных элементов транспортных объектов. При этом возникает ориентация на единство базисных характеристик предметных и исполнительных условий относительно предмета содержания и способа его реализации. Рассматривается применение основных теорем динамики точки и механической системы тел, законы сохранения и изменения базисных динамических параметров при движении составляющих морского флота.
В процессе решения системных задач динамической прикладной физики морского флота необходимо применять основные положения теории деятельности, системного анализа и теории формирования интеллекта.
Системный анализ предполагает выполнение последовательности системных аналитических действий: выделить объект анализа –динамическую задачу прикладной физики морского флота (ДЗПФМФ) как систему; установить порождающую среду ДЗПФМФ; определить уровни анализа ДЗПФМФ; представить целостные свойства ДЗПФМФ относительно пространственных, и временных характеристик и их комбинаций; выделить структуру уровня анализа ДЗПФМФ; установить структурные элементы уровня анализа ДЗПФМФ; определить системообразующие связи данного уровня анализа ДЗПФМФ; представить межуровневые связи анализа ДЗПФМФ; выделить форму организации ДЗПФМФ; установить системные свойства и поведение ДЗПФМФ.
Задача 1
Судно движется равноускоренно по спусковой дорожке стапеля, имеющей наклон 1 : 15, и проходит ее за 31 сек. Чему равен коэффициент трения, если длина спусковой дорожки 90 метров
Ответ: f = 0,048.
Задача 2
Пароход, взяв на буксир баржу водоизмещением 1000 тонн, развивает ход равноускоренно и через 80 сек имеет скорость 16 узлов. Определить натяжение буксирного троса в тот момент, когда сила сопротивления воды движению равна 1200 кН (узел – единица скорости, равная 1 миле в час, т. е. 0,5144 м/с).
Ответ: Т =1303 кН.
Задача 3
Судно водоизмещением 1800 т движется прямым курсом с ускорением a = g/6 м/с2, имея в данный момент скорость 20 узлов. Сопротивление движению корабля пропорционально квадрату скорости и при скорости в 1 м/с равно 4,9 кН. Определить упорное давление гребных винтов в рассматриваемый момент времени (узел — единица скорости, равная 1 миле в час, т. е. 0,5144 м/сек).
Ответ: F = 3460 кН .
Задача 4
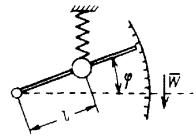
Определить вертикальное ускорение погружающегося батискафа, по упрощённой схеме акселерометра— прибора, предназначенного для измерения ускорений. если прибор показывает отклонение стрелки от горизонта на угол φ ? Пружина имеет жесткость с, расстояние от оси стрелки до груза массой m равно ℓ . Массой стрелки пренебречь. Угол φ со считать малым. Ответ: ![]() .
.


Задача 4 Задача 5
Задача 5
Судно водоизмещением m, движущееся прямым курсом, в момент включения двигателя имело скорость Vo. Считая, что величина силы упора винтов Q пропорциональна времени (Q=kt), а сила сопротивления воды Т=const, определить путь s, пройденный судном за время t1, если за это время его скорость увеличилась в два раза.
Ответ: S =  .
.
Задача 6
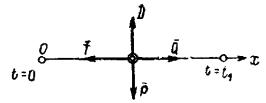
Груз, сброшенный с пикирующего самолета на высоте h на палубу корабля стоящего на рейде, имеет начальную скоростьVo, направленную под углом α к вертикали. На каком расстоянии по горизонтали от точки сбрасывания груза должен находиться корабль, чтобы груз упал на палубу корабля, если пренебречь сопротивлением воздуха?
Ответ: s =![]() .
.
Задача 7
Сила упорного давления винтов судна водоизмещением m равнаQ. Определить величину предельной скорости Vпр, которую может развить судно, а также зависимость величины его скорости от времени и Vпр, если сила сопротивления движению по величине равна ![]() . Начальную скорость судна принять равной нулю, а его движение считать прямолинейным.
. Начальную скорость судна принять равной нулю, а его движение считать прямолинейным.
Ответ: ![]() ;
; ![]() , где
, где ![]() .
.
Задача 7
Батискаф, обладая постоянной отрицательной плавучестью, погружается вертикально, испытывая сопротивление воды, пропорциональное квадрату его скорости. Определить, с какой глубины погружения h движение аппарата можно считать равномерным с относительной ошибкой ![]() , если со- предельная скорость погружения при данной плавучести, а отношение плавучести к весу батискафа равноλ. Начальная скорость равна нулю.
, если со- предельная скорость погружения при данной плавучести, а отношение плавучести к весу батискафа равноλ. Начальная скорость равна нулю.
Ответ:  .
.
Задача 8
Батискаф, обладая постоянной отрицательной плавучестью, погружается вертикально, испытывая сопротивление воды, пропорциональное квадрату его скорости. Определить время, по истечении которого погружение можно практически считать равномерным с относительной ошибкой ![]() , если со- предельная скорость погружения при данной плавучести, а отношение плавучести к весу батискафа равноλ. Начальная скорость равна нулю.
, если со- предельная скорость погружения при данной плавучести, а отношение плавучести к весу батискафа равноλ. Начальная скорость равна нулю.
Ответ: t =  .
.
Задача 9
Для взлета самолетов с судна применяют специальные катапульты, уменьшающие длину свободного пробега самолета. Считая, что действие катапульты эквивалентно дополнительной тяге, равной 4,9 кН, определить, на сколько сокра- тится длина взлетной дорожки, если масса самолета З т, тяга винта 14,71 кН, взлетная скорость 130 км/ч, а сопротивление воздуха равно 1,962V2(Н) (V = м/с).
Ответ: s = 90,3 м.
Задача 10
Судно, двигаясь прямолинейно со скоростью Vo, после остановки двигателей через некоторое время замедлило свой ход до скорости V =Vo/2. Определить среднюю скорость судна за это время, если сила сопротивления воды пропорцио- нальна его скорости.
Ответ: ![]() .
.
Задача 11
Судно, двигаясь прямолинейно со скоростью Vo, после остановки двигателей через некоторое время замедлило свой ход до скорости V =Vo/2. Определить среднюю скорость судна за это время, если сила сопротивления воды пропорциональна квадрату скорости.
Ответ: Vср = Vо ℓn 2 = 0,693Vо .
Задача 12
В момент прекращения работы двигателей судно имело скорость Vo. Определить время, прошедшее до остановки судна, если его водоизмещение равно m, а сила сопротивления R = c + kv , где (с и k — постоянные), v — скорость судна.
Ответ:  .
.
Задача 13
В момент прекращения работы двигателей судно имело скорость Vo. Определить пройденный судном путь до остановки при известном времени торможения Т (постоянная с считается неизвестной), если его водоизмещение равно m, а сила сопротивления R = c + kv , где (с и k — постоянные), v — скорость судна.
Ответ:  .
.
Задача 14
После достижения судном скорости Vo движение продолжается при постоянной мощности двигателя N, т. е. при силе упора винтов F= N/ V. Считая силу сопротивления R постоянной, определить величину предельной скорости судна Vпр и промежуток времени t1 по истечении которого будет достигнута скорость V1. Водоизмещение судна равно m.
Ответ:  .
.
Задача 15
После достижения судном скорости Vo движение продолжается при постоянной мощности двигателя N, т. е. при силе упора винтов F= N/ V. Считая силу сопротивления R постоянной, определить путь, пройденный судном за время, в течение которого его скорость изменилась от Vo до V1. Водоизмещение судна равно m.
Ответ: ![]() .
.
Задача 16
Скорость судна водоизмещением m = 25 000 тонн за время t = 50 сек после прекращения работы турбины уменьшилась на 5 узлов. Определить среднюю силу сопротивления воды, считая движение корабля прямолинейным (узел — единица скорости, равная 1 миле в час, или 0,5144 м/сек).
Ответ: 1282 кН.
Задача 17
На покоящейся непривязанной шлюпке массой m находятся два человека, массы которых равны m1 и тm2. Что произойдет со шлюпкой, если первый человек переместится по направлению к корме на расстояние ℓ1 , а второй — к носу на расстояние ℓ2 ? Сопротивлением воды пренебречь.
Ответ: шлюпка переместится на расстояние ![]() ,
,
Задача 18
Лодка с находящимся на ней человеком имеет скорость Vo. Определить, пренебрегая сопротивлением воды, перемещение s лодки вследствие движения по ней человека с относительной скоростью U по направлению к носу, если масса человека m, а масса лодки М. При каком значении U лодка не будет перемещаться?
Ответ: ![]() ;
;
лодка не будет перемещаться при ![]() .
.
Задача 19
На покоящейся лодке массой М находится человек, масса которого равна m. С какой скоростью v будет перемещаться лодка, если человек начнет двигаться по ней с относительной скоростью u ? Сопротивлением воды пренебречь.
Ответ: ![]() .
.
Задача 20
Матрос массой m перемещается по шлюпке массой М с относительной скоростью u. Определить скорость шлюпки в зависимости от времени, считая сопротивление воды постоянным и равным R. В начальный момент матрос и шлюпка находились в покое.
Ответ: ![]() .
.
Задача 21
Матрос массой m перемещается по шлюпке массой М с относительной скоростью u. Определить, через сколько времени ее скорость станет равной нулю если шлюпка получила в начальный момент скорость Vo? Какому условию должна отвечать длина шлюпки ℓ, чтобы задача имела решение при любом значении относительной скорости u ? Считать сопротивление воды постоянным и равным R. В начальный момент матрос и шлюпка находились в покое.
Ответ: ![]() .
.
Задача 22
Корабль водоизмещением 10000 тонн, двигающийся со скоростью 36 км/ч, производит залп из шести орудий по направлению, образующему с направлением движения угол 30°. Определить, на сколько процентов изменится скорость корабля в первый момент после выстрела, если считать, что поперечная составляющая отдачи уничтожается сопротивлением воды. Масса каждого снаряда 250 кг, а его начальная скорость равна 800 м/сек.
Ответ: Скорость корабля уменьшится на 1,04%.
Задача 23
Винт судна имеет момент инерции J и приводится во вращение из состояния покоя вращающим моментом М. Винт испытывает силы сопротивления воды, момент которых пропорционален квадрату угловой скорости ![]() , где k – постоянный коэффициент. Определить среднюю угловую скорость винта за промежуток времени, когда угловая скорость его станет равной ω1 .
, где k – постоянный коэффициент. Определить среднюю угловую скорость винта за промежуток времени, когда угловая скорость его станет равной ω1 .
Ответ:  .
.
Задача 24
Ротор гироскопа массой 30 кг в момент выключения делал 12 000 об/мин. Определить момент относительно оси вращения сил сопротивления, приложенных к ротору, считая их постоянными, если ротор остановился через 30 мин. Осевой радиус инерции ротора равен 10 см.
Ответ: MZ = 0,209 н.м.
Задача 25
Винт судна имеет момент инерции J и приводится во вращение из состояния покоя постоянным вращающим моментом М, встречая при этом сопротивление воды, пропорциональное его угловой скорости. Зная предельную угловую скорость ωпр , определить, через сколько времени после начала движения вращение винта можно считать равномерным с относительной ошибкой не более ![]() Ответ: через
Ответ: через ![]() .
.
Задача 26
Для уменьшения ошибок в показаниях гироскопических приборов, вызванных движением судна, приборы конструируют так, чтобы период собственных колебаний был равен периоду колебаний математического маятника, имеющего длину, равную радиусу Земли (R = 6400 км). Определить этот период.
Ответ: Т = 84 мин .
Задача 27
Шлюпка вместе с гребцами имеет массу 800 кг. Считая, что каждый гребец прикладывает к рукоятке весла силу 100 н, перемещая ее при этом на 1 м, найти, какую скорость сообщают шлюпке восемь гребцов после пяти размахов. Сопротивлением воды пренебречь.
Ответ: v = 3,16 м/сек.
Задача 28
Судно должно спускаться со стапеля на воду по наклонным спусковым путям длиной s. Определить угол α наклона путей к горизонту так, чтобы скорость судна в конце спуска не превосходила v, если угол трения φ = const.
Ответ: ![]() .
.
Задача 29
Буксир А водоизмещением m1 тянет две баржи В и С, водоизмещения которых соответственно равны m2 и m3 . Определить силу упора винтов буксира Q, если он движется прямолинейным курсом с ускорением a . Общая сила сопротивления движению системы равна R.![]() Ответ:Q=R+(m1+m2+m3)a
Ответ:Q=R+(m1+m2+m3)a
Литература
Н. А. Бражниченко и др. Сборник задач по теоретической механике. М.: 1967. – С.528
Источник
Физика /1.Теоретическая физика
К.п.н. Мищик С.А.
Государственный морской университет имени
адмирала Ф.Ф.Ушакова ,
Россия
Системные задачи динамической прикладной физики
морского флота
Системные задачи динамической прикладной
физики морского флота отражают целостно-системное моделирование основных
элементов транспортных объектов. При этом возникает ориентация на единство
базисных характеристик предметных и исполнительных условий относительно
предмета содержания и способа его реализации. Рассматривается применение
основных теорем динамики точки и механической системы тел, законы сохранения и
изменения базисных динамических параметров при движении составляющих морского
флота.
В процессе решения системных задач динамической
прикладной физики морского флота необходимо применять основные положения теории
деятельности, системного анализа и теории формирования интеллекта.
Системный анализ предполагает
выполнение последовательности системных аналитических действий: выделить объект
анализа –динамическую задачу прикладной физики морского флота (ДЗПФМФ) как
систему; установить порождающую среду ДЗПФМФ; определить уровни анализа ДЗПФМФ;
представить целостные свойства ДЗПФМФ относительно пространственных, и временных
характеристик и их комбинаций; выделить структуру уровня анализа ДЗПФМФ;
установить структурные элементы уровня анализа ДЗПФМФ; определить
системообразующие связи данного уровня анализа ДЗПФМФ; представить межуровневые
связи анализа ДЗПФМФ; выделить форму организации ДЗПФМФ; установить системные
свойства и поведение ДЗПФМФ.
Задача 1
Судно
движется равноускоренно по спусковой дорожке стапеля, имеющей наклон 1 : 15, и
проходит ее за 31 сек. Чему равен коэффициент трения, если длина спусковой
дорожки 90 метров
Ответ:
f
= 0,048.
Задача 2
Пароход, взяв на буксир баржу водоизмещением 1000 тонн,
развивает ход равноускоренно и через 80 сек имеет скорость 16 узлов. Определить
натяжение буксирного троса в тот момент, когда сила сопротивления воды движению
равна 1200 кН (узел – единица скорости, равная 1 миле в час, т. е. 0,5144 м/с).
Ответ: Т =1303 кН.
Задача 3
Судно
водоизмещением 1800 т движется прямым курсом с ускорением a = g/6 м/с2, имея в данный момент скорость 20 узлов.
Сопротивление движению корабля пропорционально квадрату скорости и при скорости
в 1 м/с равно 4,9 кН. Определить упорное давление гребных винтов в
рассматриваемый момент времени (узел — единица скорости, равная 1 миле в час, т.
е. 0,5144 м/сек).
Ответ:
F = 3460 кН .
Задача 4
Определить
вертикальное ускорение погружающегося батискафа, по упрощённой схеме акселерометра—
прибора, предназначенного для измерения ускорений. если прибор показывает
отклонение стрелки от горизонта на угол φ ? Пружина имеет жесткость с,
расстояние от оси стрелки до груза массой m
равно ℓ . Массой стрелки
пренебречь. Угол φ со
считать малым. Ответ: ![]() .
.
Задача 4 Задача 5
Задача 5
Судно
водоизмещением m, движущееся прямым курсом, в момент включения
двигателя имело скорость Vo. Считая, что
величина силы упора винтов Q пропорциональна
времени (Q=kt), а сила сопротивления
воды Т=const, определить путь s, пройденный судном
за время t1, если за это время
его скорость увеличилась в два раза.
Ответ:
S = 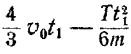 .
.
Задача 6
Груз, сброшенный с
пикирующего самолета на высоте h на палубу корабля стоящего на рейде, имеет начальную
скоростьVo, направленную под углом α к вертикали. На каком расстоянии по горизонтали от
точки сбрасывания груза должен находиться корабль, чтобы груз упал на палубу корабля,
если пренебречь сопротивлением воздуха?
Ответ: s
=![]() .
.
Задача 7
Сила упорного давления
винтов судна водоизмещением m равнаQ.
Определить величину предельной скорости Vпр, которую может развить судно, а также зависимость
величины его скорости от времени и Vпр, если сила сопротивления движению по величине равна ![]() . Начальную скорость судна принять равной нулю, а его
. Начальную скорость судна принять равной нулю, а его
движение считать прямолинейным.
Ответ: ![]() ;
; ![]() , где
, где ![]() .
.
Задача 7
Батискаф, обладая
постоянной отрицательной плавучестью, погружается вертикально, испытывая
сопротивление воды, пропорциональное квадрату его скорости. Определить, с какой
глубины погружения h движение аппарата можно считать равномерным с
относительной ошибкой ![]() , если со- предельная скорость погружения при данной
, если со- предельная скорость погружения при данной
плавучести, а отношение плавучести к весу батискафа равно λ.
Начальная скорость равна нулю.
Ответ: 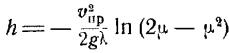 .
.
Задача 8
Батискаф, обладая
постоянной отрицательной плавучестью, погружается вертикально, испытывая
сопротивление воды, пропорциональное квадрату его скорости. Определить время,
по истечении которого погружение можно практически считать равномерным с
относительной ошибкой ![]() , если со- предельная скорость погружения при данной
, если со- предельная скорость погружения при данной
плавучести, а отношение плавучести к весу батискафа равно λ.
Начальная скорость равна нулю.
Ответ: t = 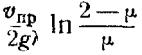 .
.
Задача 9
Для взлета самолетов с
судна применяют специальные катапульты, уменьшающие длину свободного пробега
самолета. Считая, что действие катапульты эквивалентно дополнительной тяге,
равной 4,9 кН, определить, на сколько сокра- тится длина взлетной дорожки, если
масса самолета З т, тяга винта 14,71 кН, взлетная скорость 130 км/ч, а
сопротивление воздуха равно 1,962V2(Н) (V = м/с).
Ответ: s = 90,3
м.
Задача 10
Судно, двигаясь
прямолинейно со скоростью Vo, после остановки двигателей через некоторое время
замедлило свой ход до скорости V =Vo/2. Определить среднюю скорость судна за это время,
если сила сопротивления воды пропорцио- нальна его скорости.
Ответ: ![]() .
.
Задача 11
Судно, двигаясь
прямолинейно со скоростью Vo, после остановки двигателей через некоторое время
замедлило свой ход до скорости V =Vo/2. Определить среднюю скорость судна за это время,
если сила сопротивления воды пропорциональна квадрату скорости.
Ответ: Vср = Vо ℓn 2 = 0,693Vо .
Задача 12
В момент прекращения
работы двигателей судно имело скорость Vo. Определить
время, прошедшее до остановки судна, если его водоизмещение равно m, а
сила сопротивления R = c + kv , где (с и k —
постоянные), v — скорость
судна.
Ответ: 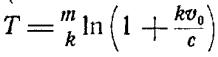 .
.
Задача 13
В момент прекращения
работы двигателей судно имело скорость Vo. Определить
пройденный судном путь до остановки при известном времени торможения Т
(постоянная с считается неизвестной), если его водоизмещение равно m, а
сила сопротивления R = c + kv , где (с и k —
постоянные), v — скорость
судна.
Ответ: 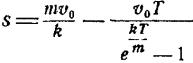 .
.
Задача 14
После достижения
судном скорости Vo движение
продолжается при постоянной мощности двигателя N, т. е. при силе упора
винтов F= N/ V. Считая силу сопротивления R постоянной, определить
величину предельной скорости судна Vпр и промежуток времени t1 по истечении которого будет достигнута скорость V1. Водоизмещение судна равно m.
Ответ: 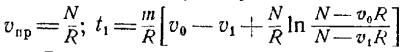 .
.
Задача 15
После достижения
судном скорости Vo движение
продолжается при постоянной мощности двигателя N, т. е. при силе упора
винтов F= N/ V. Считая силу сопротивления R постоянной, определить путь,
пройденный судном за время, в течение которого его скорость изменилась от Vo до V1. Водоизмещение судна равно m.
Ответ: ![]() .
.
Задача 16
Скорость судна
водоизмещением m = 25 000 тонн за время t = 50 сек после прекращения работы турбины уменьшилась
на 5 узлов. Определить среднюю силу сопротивления воды, считая движение корабля
прямолинейным (узел — единица скорости, равная 1 миле в час, или 0,5144 м/сек).
Ответ: 1282 кН.
Задача 17
На покоящейся
непривязанной шлюпке массой m находятся два человека, массы
которых равны m1 и тm2.
Что произойдет со шлюпкой, если первый человек переместится по направлению к
корме на расстояние ℓ1 , а второй — к носу на расстояние ℓ2 ? Сопротивлением воды пренебречь.
Ответ: шлюпка
переместится на расстояние ![]() ,
,
Задача 18
Лодка с находящимся на
ней человеком имеет скорость Vo. Определить, пренебрегая сопротивлением воды, перемещение
s лодки вследствие движения по ней человека с относительной скоростью U по направлению к носу, если масса человека m,
а масса лодки М. При каком значении U лодка не будет перемещаться?
Ответ: ![]() ;
;
лодка не будет
перемещаться при ![]() .
.
Задача 19
На покоящейся лодке
массой М находится человек, масса которого равна m. С какой скоростью v
будет перемещаться лодка, если человек начнет двигаться по ней с относительной
скоростью u ? Сопротивлением воды пренебречь.
Ответ: ![]() .
.
Задача 20
Матрос массой m
перемещается по шлюпке массой М с относительной скоростью u.
Определить скорость шлюпки в зависимости от времени, считая сопротивление воды
постоянным и равным R. В начальный момент матрос и шлюпка находились в покое.
Ответ: ![]() .
.
Задача 21
Матрос массой m
перемещается по шлюпке массой М с относительной скоростью u.
Определить, через сколько времени ее скорость станет равной нулю если шлюпка получила
в начальный момент скорость Vo? Какому условию должна отвечать длина шлюпки ℓ, чтобы задача имела решение
при любом значении относительной скорости u ? Считать сопротивление воды постоянным и равным R.
В начальный момент матрос и шлюпка находились в покое.
Ответ: ![]() .
.
Задача 22
Корабль водоизмещением
10000 тонн, двигающийся со скоростью 36 км/ч, производит залп из шести орудий
по направлению, образующему с направлением движения угол 30°. Определить, на
сколько процентов изменится скорость корабля в первый момент после выстрела,
если считать, что поперечная составляющая отдачи уничтожается сопротивлением
воды. Масса каждого снаряда 250 кг, а его начальная скорость равна 800 м/сек.
Ответ: Скорость корабля
уменьшится на 1,04%.
Задача 23
Винт судна имеет
момент инерции J и
приводится во вращение из состояния покоя вращающим моментом М. Винт
испытывает силы сопротивления воды, момент которых пропорционален квадрату
угло
