Для откорма животных употребляют 2 вида кормов
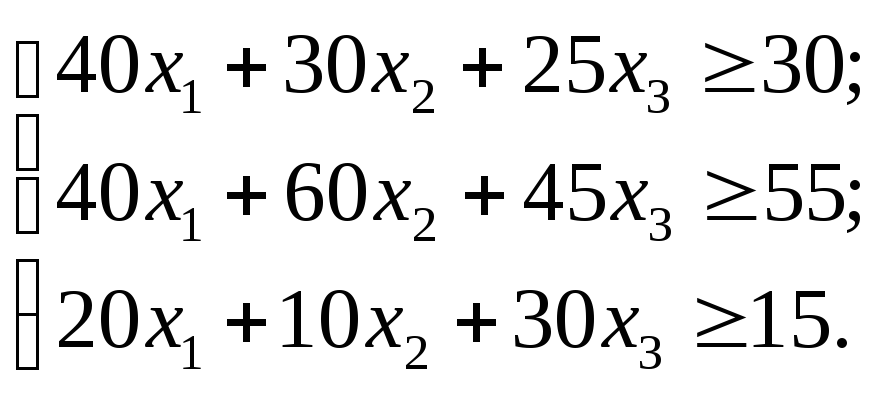
Вариант № 2.
Задача № 1. Решить графическим методом типовую задачу оптимизации.
Совхоз для кормления животных использует два вида корма. В дневном рационе животного должно содержаться не менее 6 единиц питательного вещества ![]() и не менее 12 единиц питательного вещества
и не менее 12 единиц питательного вещества ![]() . Какое количество корма надо расходовать ежедневно на одного животного, чтобы затраты были минимальными? Использовать данные таблицы:
. Какое количество корма надо расходовать ежедневно на одного животного, чтобы затраты были минимальными? Использовать данные таблицы:

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на максимум и почему?
Решение:
1. Введем переменные:
![]() – количество корма 1;
– количество корма 1;
![]() – количество корма 2.
– количество корма 2.
2. Зададим целевую функцию. Задача на минимизацию затрат. Запишем уравнение, описывающее затраты
![]()
3. Ограничения:

Найдем решение сформированной задачи, используя ее геометрическую интерпретацию. Сначала определим область допустимых решений. Для этого в неравенствах системы ограничений знаки неравенств заменим на знаки точных равенств, и найдем соответствующие прямые:

Выразим ![]() через
через ![]()

Для построения прямой достаточно двух точек, найдем их координаты:

Эти прямые изображены на рисунке 1. Условие неотрицательности показывает, что искомая область располагается в первой четверти.
Каждая из построенных прямых делит плоскость на две полуплоскости. Координаты точек одной полуплоскости удовлетворяют исходному неравенству, а другой – нет. Чтобы определить искомую полуплоскость, нужно взять какую-нибудь точку, принадлежащую одной из полуплоскостей, и проверить, удовлетворяют ли ее координаты данному неравенству. Если координаты взятой точки удовлетворяют данному неравенству, то искомой является та полуплоскость, которой принадлежит эта точка, в противном случае – другая полуплоскость.

Рисунок 1. Графический метод решения
На рисунке 1, область допустимых решений не ограничена и отмечена штрихом. Координаты любой точки, принадлежащей этой области, удовлетворяют данной системе неравенств и условию неотрицательности переменных. Поэтому сформулированная задача будет решена, если мы сможем найти точку, принадлежащую области допустимых решений, в которой целевая функция принимает минимальное значение. Чтобы найти указанную точку, построим вектор ![]() и линию уровня, которая перпендикулярна этому вектору.
и линию уровня, которая перпендикулярна этому вектору.
Так как задача на минимум, то линию уровня будем двигать по направлению вектора. Первая точка касания и будет оптимальным решением. Координаты этой точки и определяют оптимальные количества кормов ![]() и
и ![]() , при которых ежедневные затраты на кормление одного животного являются минимальными.
, при которых ежедневные затраты на кормление одного животного являются минимальными.
В данном примере это точка пересечения прямых I и ![]() Следовательно, ее координаты удовлетворяют уравнениям этих прямых
Следовательно, ее координаты удовлетворяют уравнениям этих прямых
![]()
Следовательно, если совхоз для кормления животных будет использовать 2 кг корма 1 и 2 кг корма 2, то минимальные затраты составят ![]()
Если данную задачу решать на максимум, то линия уровня будет сдвигаться вправо до бесконечности (так область решений не ограничена). Таким образом, конечного решения не будет.
Задача № 2. Предложить оптимальное управленческое решение в следующих типовых хозяйственных ситуациях.
В обработку поступили две партии досок для изготовления комплектов из трех деталей (треугольные каркасы настилов на стройплощадку), причем первая партия содержит 52 доски длиной по 6,5 м каждая, вторая содержит 200 досок длиной по 4 м каждая. Каждый комплект состоит из двух деталей по 2 м каждая и одной детали в 1,25 м.
Ставится задача поиска рационального варианта раскроя поступившего в обработку материала.
Решение:
Критерием оптимальности в данной задаче будет максимум выпуска комплектной продукции. Построим возможные способы раскроя исходного материала:

Введем необходимые обозначения: ![]() – число досок из
– число досок из ![]() партии
партии ![]() , которое следует раскроить
, которое следует раскроить ![]() способом. Рассмотрим соотношения:
способом. Рассмотрим соотношения:
![]()
![]()
Обозначим через ![]() – минимальное из этих соотношений (это и будет количество комплектной продукции). Следовательно, экономико-математическая модель примет вид:
– минимальное из этих соотношений (это и будет количество комплектной продукции). Следовательно, экономико-математическая модель примет вид:
![]()
![]()
![]()
![]()
![]() – Целые неотрицательные. Для удобства записи заменим двухиндексные переменные
– Целые неотрицательные. Для удобства записи заменим двухиндексные переменные ![]() на одноиндексные переменные
на одноиндексные переменные ![]() так как это показано в таблице раскроя
так как это показано в таблице раскроя ![]() Тогда ЭММ задачи примет вид:
Тогда ЭММ задачи примет вид:
![]()
При ограничениях:
![]()
![]()
![]()
![]()
![]()
Реализуя приведенную модель в любом пакете прикладных программ, получим решение:
![]()
Оптимальные значения остальных переменных равны нулю. Следовательно, в данной хозяйственной ситуации максимальное количество наборов, равное 215 шт. можно изготовить и реализовать, если:
– раскроить каждую из 15 досок длиной 6,5 м на 2 детали по 2 м и 2 детали по 1,25 м;
– раскроить каждую из 37 досок длиной 6,5 м на 5 деталей по 1,25 м;
– раскроить каждую из 200 досок длиной 4 м на 2 детали по 2 м. В этом случае будет получена максимальная выручка.
Задача № 3. Провести моделирование и решить специальную задачу линейного программирования.
Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить ремонтные работы на пяти участках автодорог. Песок на участки ремонтных работ может доставляться из трех карьеров, месячные объемы предложений по карьерам известны. Из планов производства ремонтных работ известны месячные объемы потребностей по участкам работ. Имеются экономические оценки транспортных затрат (в у. е.) на перевозку 1тонны песка с карьеров на ремонтные участки.
Числовые данные для решения содержатся ниже в Матрице планирования. Требуется:
1) Предложить план перевозок песка на участки ремонта автодорог, который обеспечивает минимальные совокупные транспортные издержки.
2) Что произойдет с оптимальным планом, если изменятся условия перевозок: а) появится запрет на перевозки от первого карьера до второго участка работ?; б) по этой коммуникации будет ограничен объем перевозок 3 тоннами?
Матрица планирования:

Решение:
Суммарные объемы предложений по карьерам равны суммарным объемам потребностей по участкам работ, т. е. выполняется условие общего баланса ![]() Следовательно, данная задача закрытого типа.
Следовательно, данная задача закрытого типа.
Построим начальный базисный план Методом минимальной стоимости. Назначение перевозок начинаем с клетки (1,5), имеющей минимальную стоимость перевозки (1). В клетку (1,5) записываем наименьшее из значений ![]() и
и ![]()
![]() и исключаем из дальнейшего рассмотрения пятый участок. Корректируем предложение первого карьера на величину
и исключаем из дальнейшего рассмотрения пятый участок. Корректируем предложение первого карьера на величину ![]()
Следующая поставка осуществляется от второго карьера третьему участку. В клетку (2,3) назначаем перевозку ![]() исключаем из дальнейшего рассмотрения третий участок. Корректируем предложение второго карьера
исключаем из дальнейшего рассмотрения третий участок. Корректируем предложение второго карьера ![]() С оставшейся матрицей поступаем аналогично предыдущему:
С оставшейся матрицей поступаем аналогично предыдущему:
![]()
![]()
![]()
![]()
План перевозок, построенный методом минимальной стоимости:

Построенный начальный план перевозок является вырожденным, так как число назначенных перевозок ![]() меньше
меньше ![]() В одну из свободных клеток поставим ноль. Определим полную стоимость перевозок по найденному опорному плану:
В одну из свободных клеток поставим ноль. Определим полную стоимость перевозок по найденному опорному плану:
![]()
Определим оптимальность полученного плана. С помощью Метода потенциалов вычислим потенциалы строк и столбцов по стоимости перевозок в загруженных клетках. Если известен ![]() , то
, то ![]() если известен
если известен ![]() , то
, то ![]() Положим, например,
Положим, например, ![]() Тогда будут вычислены и остальные потенциалы строк и столбцов.
Тогда будут вычислены и остальные потенциалы строк и столбцов.
![]()
![]()
![]()
![]()

Для незагруженных клеток вычислим величины превышения стоимости ![]()
![]()
![]()
![]()
![]()
Полученный план не оптимален. Среди оценок ![]() имеется отрицательное значение. Потенциальной является клетка
имеется отрицательное значение. Потенциальной является клетка ![]() . От клетки
. От клетки ![]() строим замкнутый контур:
строим замкнутый контур: ![]() Начиная с клетки
Начиная с клетки ![]() разметим вершины контура попеременно знаками плюс «+», минус «-», обходя замкнутый контур в любом направлении. Из клеток, помеченных знаком «-», выбираем наименьшее значение объема перевозки
разметим вершины контура попеременно знаками плюс «+», минус «-», обходя замкнутый контур в любом направлении. Из клеток, помеченных знаком «-», выбираем наименьшее значение объема перевозки ![]() Сформируем новый улучшенный план: на 100 увеличим перевозки в клетках, помеченных знаком «+», и уменьшим в клетках, помеченных знаком «-».
Сформируем новый улучшенный план: на 100 увеличим перевозки в клетках, помеченных знаком «+», и уменьшим в клетках, помеченных знаком «-».

Определим полную стоимость перевозок по новому плану ![]()
![]()
Вычислим потенциалы и величины превышения стоимости для незагруженных клеток:
![]()
![]()
![]()
![]()
Полученный план не оптимален. Среди оценок ![]() имеется отрицательное значение. Потенциальной является клетка
имеется отрицательное значение. Потенциальной является клетка ![]() . От клетки
. От клетки ![]() строим замкнутый контур:
строим замкнутый контур: ![]() Выбираем наименьшее значение объема перевозки
Выбираем наименьшее значение объема перевозки ![]() Сформируем новый улучшенный план: на 0 увеличим перевозки в клетках, помеченных знаком «+», и уменьшим в клетках, помеченных знаком «-».
Сформируем новый улучшенный план: на 0 увеличим перевозки в клетках, помеченных знаком «+», и уменьшим в клетках, помеченных знаком «-».

Определим полную стоимость перевозок по новому плану ![]()
![]()
Вычислим потенциалы и величины превышения стоимости для незагруженных клеток:
![]()
![]()
![]()
![]()
Характеристики свободных клеток не отрицательны, следовательно, текущий план оптимален.
Выясним, что произойдет с оптимальным планом, если появится запрет на перевозки от первого карьера до второго участка работ. В этом случае, будем считать, что транспортные затраты на перевозку от первого карьера до второго участка работ бесконечно большая ![]() . Составим начальный план методом минимальной стоимости в столбце.
. Составим начальный план методом минимальной стоимости в столбце.

Построенный начальный план перевозок является невырожденным, так как число назначенных перевозок ![]() равно
равно ![]() Определим полную стоимость перевозок по найденному опорному плану:
Определим полную стоимость перевозок по найденному опорному плану:
![]()
Определим оптимальность полученного плана с помощью Метода потенциалов.

Для незагруженных клеток вычислим величины превышения стоимости ![]()
![]()
![]()
![]()
![]()
Характеристики свободных клеток не отрицательны, следовательно, текущий план оптимален. Таким образом, при запрете на перевозку с первого карьера на второй участок, транспортные расходы вырастут на ![]()
Выясним, что произойдет с оптимальным планом, если перевозка от первого карьера до второго участка работ будет ограничена объемом 3 тонны. Составим начальный план произвольным образом, учитывая данное ограничение.

Построенный начальный план перевозок является невырожденным, так как число базисных клеток (без ограничений на перевозку) ![]() равно
равно ![]() Определим полную стоимость перевозок по найденному опорному плану:
Определим полную стоимость перевозок по найденному опорному плану:
![]()
Определим оптимальность полученного плана с помощью Метода потенциалов.

Для незагруженных клеток вычислим величины превышения стоимости ![]()
![]()
![]()
![]()
![]()
Полученный план не оптимален. Среди оценок ![]() имеются отрицательные значения. Потенциальной является клетка
имеются отрицательные значения. Потенциальной является клетка ![]() . От клетки
. От клетки ![]() строим замкнутый контур:
строим замкнутый контур: ![]() Выбираем наименьшее значение объема перевозки
Выбираем наименьшее значение объема перевозки ![]() Сформируем новый улучшенный план.
Сформируем новый улучшенный план.

Определим полную стоимость перевозок по найденному опорному плану:
![]()
Для незагруженных клеток вычислим величины превышения стоимости ![]()
![]()
![]()
![]()
![]()
Полученный план не оптимален. Среди оценок ![]() имеются отрицательные значения. Потенциальной является клетка
имеются отрицательные значения. Потенциальной является клетка ![]() . От клетки
. От клетки ![]() строим замкнутый контур:
строим замкнутый контур: ![]() Выбираем наименьшее значение объема перевозки
Выбираем наименьшее значение объема перевозки ![]() Сформируем новый улучшенный план.
Сформируем новый улучшенный план.

Определим полную стоимость перевозок по найденному опорному плану:
![]()
Для незагруженных клеток вычислим величины превышения стоимости ![]()
![]()
![]()
![]()
![]()
Характеристики свободных клеток не отрицательны (кроме клетки с ограничением), следовательно, текущий план оптимален. Таким образом, при ограничении на перевозку с первого карьера на второй участок тремя тоннами, транспортные расходы вырастут на ![]()
Задача № 4. Рассчитать характеристики системы массового обслуживания. Поток требований является простейшим (пуассоновским), а продолжительность обслуживания распределена по экспоненциальному закону.
На строительном участке в инструментальной мастерской работают 3 мастера. Если рабочий заходит в мастерскую, когда все мастера заняты обслуживанием ранее обратившихся работников, то он не уходит из мастерской и ожидает обслуживания. Статистика показала, что среднее число рабочих, обращающихся в мастерскую в течение часа, равно 4, среднее время, которое затрачивает мастер на заточку или ремонт инструмента, равно 10 мин. Рассчитайте основные характеристики работы данной мастерской как СМО с ожиданием.
Решение:
Имеем
![]()
Тогда интенсивность обслуживания равна
![]()
Интенсивность нагрузки равна
![]()
Поскольку
![]()
Очередь не растет безгранично и имеет смысл говорить о предельном стационарном режиме работы СМО. Находим вероятности состояний:


Число занятых каналов найдем, разделив абсолютную пропускную способность СМО ![]() на интенсивность обслуживания
на интенсивность обслуживания ![]()
![]()
Вероятность отсутствия очереди будет:
![]()
Среднее число рабочих в очереди:

Среднее число рабочих в мастерской:
![]()
Среднее время ожидания в очереди:
![]()
Среднее время пребывания рабочего в мастерской:
![]()
Источник
Поиск
оптимальных решений в MSExcel.
Экономические приложения
Задача о смесях
(рационе, диете)
К группе задач о смесях
относят задачи по отысканию наиболее
дешевого набора из определенных исходных
материалов, обеспечивающих получение
смеси с заданными свойствами. Иными
словами, получаемые смеси должны иметь
в своем составе несколько различных
компонентов в определенных количествах,
а сами компоненты являются составными
частями нескольких исходных материалов.
Постановка
задачи
Предприятию
требуется изготовить некоторое количество
сплава, содержащего не менее 15 компонент
олова, 55 компонент цинка и 30 компонент
свинца. Требуемый сплав изготавливается
из трех исходных сплавов, в которых
содержатся вышеуказанные составляющие.
Данные о содержании олова, цинка и свинца
в исходных материалах приведены в
таблице, там же задана стоимость единицы
каждого сплава.
Следует
определить, какие из исходных сплавов
и в каких количествах нужно использовать
для получения требуемого сплава, чтобы
суммарные затраты на исходные сплавы
были минимальными.
Составляющие | Кол-во | Необходимое | ||
Сплав | Сплав | Сплав | ||
Свинец | 40 | 30 | 25 | 30 |
Цинк | 40 | 60 | 45 | 55 |
Олово | 20 | 10 | 30 | 15 |
Цена | 50 | 40 | 70 | |
Разработка
математической модели
Обозначим
через x1,
x2,
x3
количество единиц исходных сплавов
Сплава 1, Сплава 2 и Сплава 3 в требуемом
сплаве. Цель данной задачи – добиться
минимальных затрат на изготовление
требуемого сплава, поэтому общую
стоимость требуемого сплава можно
выразить в виде линейной функции
![]()
Принимая
во внимание данные приведенные в таблице
и условие, что требуемый сплав должен
содержать составляющих компонентов не
менее указанного, получаем систему
ограничений:
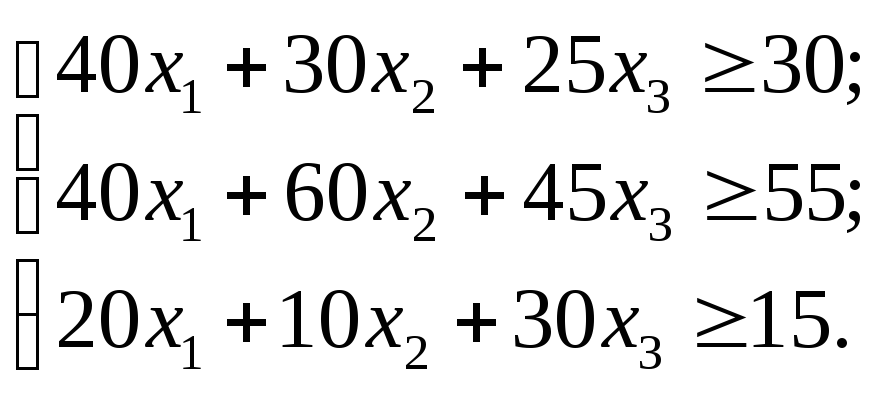
Если
Сплав 1 не используется в требуемом
сплаве, то
![]() в
в
противном случае x1
больше 0. Аналогично имеем
![]() и
и
![]() ,
,
т.е. должно выполняться условие
неотрицательности переменных.
Математическая
модель задачи выглядит следующим
образом.
Целевая
функция имеет вид:
![]()
ЦФ
представляет стоимость требуемого
сплава.
Ограничения
имеют вид:
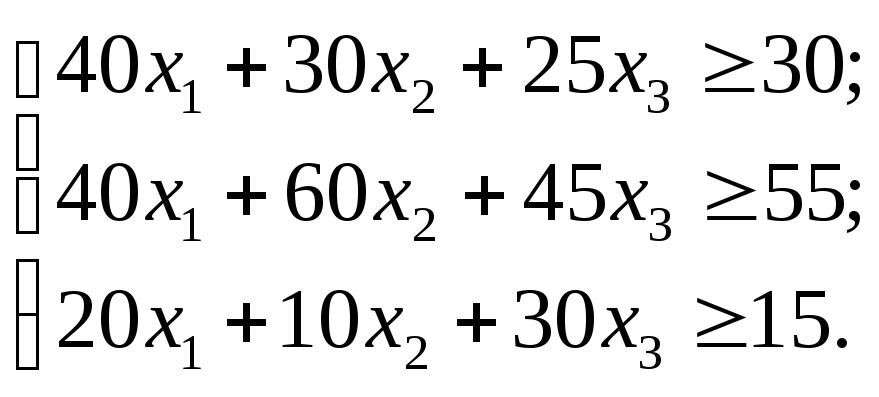
Ограничения
задачи представляют содержание
компонентов в сплаве, требуемый сплав
должен содержать компоненты в объемах,
не менее указанных.
Граничные
условия
![]()
представляют тот факт, количество
исходных сплавов не может быть
отрицательным.
Вид
электронной таблицы созданной для
решения задачи, представлен на рисунке.


Поиск
оптимального решения выполнить
самостоятельно.
Результат
поиска решения

Самостоятельная работа
1.
Для откорма животных употребляют два
корма: 1 и 2. Стоимость одного килограмма
корма 1 – 5 руб., корма 2 – 2 руб. В каждом
килограмме корма 1 содержится 5 ед.
витамина А, 2,5 ед. витамина В и 1 ед.
витамина С. В каждом килограмме корма
2 содержится 3 ед. витамина А, 3 ед. витамина
В и 1 ед. витамина С.
Какое
количество корма каждого вида необходимо
расходовать ежедневно, чтобы затраты
на откорм были минимальными, если
суточный рацион предусматривает не
менее 225 питательных единиц витамина
А, не менее 150 ед. витамина В и не менее
80 ед. витамина С?
2. Чтобы при откорме
животных весом 30-40 кг получить средний
привес 300-400 г, по нормам в дневном рационе
должны содержаться питательные вещества
в следующем количестве: кормовых единиц
– не менее 1,6 кг; переваримого протеина
– не менее 200 г, каротина – не менее 10
мг. При откорме используют ячмень, бобы
и сенную муку. Содержание питательных
веществ в 1 кг этих кормов и стоимости
1 кг корма приведены в
таблице.
Составить дневной
рацион, удовлетворяющий данной
питательности при минимальной стоимости.
Наименование питательного | Количество в | ||
ячмень | бобы | сенная | |
Кормовые | 1,2 | 1,4 | 0,8 |
Переваримый | 80 | 280 | 240 |
Каротин, | 5 | 5 | 100 |
Цена | 3 | 4 | 5 |
3. На птицеферме
употребляется два вида кормов – I и II.
В единице веса корма I содержится единица
вещества А, единица вещества В и единица
вещества С. В единице веса корма II
содержатся четыре единицы вещества А,
две единицы вещества В и не содержится
вещество С. В дневной рацион каждой
птицы надо включить не менее единицы
вещества А, не менее четырех единиц
вещества В и не менее единицы вещества
С. Цена единицы веса корма I составляет
30 руб., корма II – 20 руб. Составить ежедневный
рацион кормления птицы таким образом,
чтобы обеспечить наиболее дешевый
рацион питания.
4. Для поддержания
нормальной жизнедеятельности человеку
ежедневно необходимо потреблять не
менее 118 г белков, 56 г жиров, 500 г углеводов,
8 г минеральных солей. Количество
питательных веществ, содержащихся в 1
кг каждого вида потребляемых продуктов,
а также цена 1 кг каждого из этих продуктов
приведены в следующей таблице:
Питательные вещества | Содержание | ||||||
мясо | рыба | молоко | масло | сыр | крупа | картофель | |
Белки | 180 | 190 | 30 | 10 | 260 | 130 | 21 |
Жиры | 20 | 3 | 40 | 865 | 310 | 30 | 2 |
Углеводы | – | – | 50 | 6 | 20 | 650 | 200 |
Минеральные | 9 | 10 | 7 | 12 | 60 | 20 | 10 |
Цена, | 1,8 | 1,0 | 0,28 | 3,4 | 2,9 | 0,5 | 0,1 |
Составить дневной
рацион, содержащий не менее суточной
нормы потребности человека в необходимых
питательных веществах при минимальной
общей стоимости потребляемых продуктов.
5. Фирма выпускает два
набора удобрений для газонов: обычный
и улучшенный. В обычный набор входит 3
кг азотных, 4 кг фосфорных и 1 кг калийных
удобрений, а в улучшенный – 2 кг
азотных, 6 кг фосфорных и 3 кг калийных
удобрений. Известно, что для газона
требуется, по меньшей мере, 10 кг азотных,
20 кгфосфорных и 7 кг калийных
удобрений. Обычный набор стоит 3 д.ед.,
а улучшенный – 4 д.ед. Какие и сколько
наборов удобрений нужно купить, чтобы
обеспечить эффективное питание почвы
и минимизировать стоимость?
6. Для откорма животных
в хозяйстве употребляют два вида кормов:
N1, N2, стоимость корма N1 – 500 ден.ед./кг,
корма N2 – 300 ден.ед./кг. Корм N1 содержит
5 ед/кг вещества А, 4 ед/кг вещества В, 2
ед/кг вещества С, корм N2 содержит
соответственно 6, 5, 3 ед/кг этих веществ.
Ежедневно может быть расходовано до 4
кг кормов каждого вида. Какое количество
корма каждого вида необходимо расходовать
ежедневно, чтобы затраты на откорм были
минимальными, если суточный рацион
должен содержать вещества А – не более
40 ед., вещества В – не менее 16 ед., вещества
С – не менее 17 ед.
7. Для кормления телят
фермер располагает двумя видами кормов:
комбикорм и ячмень молотый. Один килограмм
комбикорма дает 300 г привеса, ячменя
молотого – 100 г привеса. Комбикорм
содержит 20% сухого вещества, 2% протеина,
1% кальция, ячмень молотый – 50% сухого
вещества, 1% протеина, 2% кальция. Исходя
из максимального привеса, рассчитать
оптимальный суточный рацион из этих
двух видов кормов, если в нем (по норме)
должно содержаться не более 1 кг сухого
вещества, не менее 60 г протеина и не
менее 20 г кальция.
8. Современному
культурному фермеру Иванову (бывший
председатель колхоза “Серпом по
молоту”) необходимо внести минеральные
удобрения под новую для него сельхозкультуру.
По новым рекомендациям под эту
культуру в расчете на один гектар надо
вносить 10 кг азота, 8 кг фосфора и 5 кг
калия. На рынке имеется четыре вида
подходящих удобрений разных производителей.
Содержание необходимых элементов в
килограммах и цена в расчете на 1 тонну
для этих видов удобрения показаны в
следующей таблице.
Удобрение | Содержание | Цена, руб. | ||
азота | фосфора | калия | ||
1 | 26 | 12 | 4 | 550 |
2 | 12 | 6 | 10 | 450 |
3 | 8 | 10 | 5 | 350 |
4 | 5 | 12 | 4 | 300 |
Допустим, фермер Иванов
просит Вас как крупного специалиста по
принятию решений подсчитать, сколько
ему нужно купить удобрения каждого
типа и в каких пропорциях их смешивать,
чтобы было подешевле и чтобы содержание
необходимых элементов в смеси было не
меньше, чем советуют ученые. Всего Иванов
планирует внести эти удобрения на 90
гектаров.
5
КИТ, ЭКФАК, НИСПО, 2 КУРС,
ЗАОЧНОЕ
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
